Recently, Associate Professor Yong-Chun Liu of the Department of Physics and others have found the hybrid skin-topological effect induced by gain and loss and the parity-time phase transition between skin-topological modes. The research results were published in Physical Review Letters under the title of "Gain-loss-induced hybrid skin-topological effect".
Non-Hermitian systems are open systems that can be described by non-Hermitian Hamiltonians. There are many novel properties in non-Hermitian systems, one of which is the non-Hermitian skin effect. In this effect, all the eigenstates of a topological system (including bulk states and edge states) are localized to one of the system boundaries, and the conventional bulk-edge correspondence is broken down. There are mainly two ways to realize non-Hermitian systems: one is using non-reciprocal couplings, and the other is using gain and loss. In the case of non-reciprocal couplings, the non-Hermiticity comes from the non-Hermitian nature of the interaction between different lattice sites. The energy exchange between the lattice sites is asymmetric, so there is a net energy flow in one direction and all the energy is finally gathered on the boundary. Thus, the non-reciprocal systems exhibit the skin effect. In the case of gain-loss, the non-Hermiticity originates from the gain and loss at each lattice site, which is equivalent to adding imaginary on-site energy to each lattice site. This kind of non-Hermitian system does not always lead to the skin effect. In realistic systems, non-reciprocal couplings are usually difficult to achieve, but dissipation is widespread, and staggered dissipation distribution is equivalent to gain and loss. Therefore, it is of great significance to study the skin effect in gain-loss non-Hermitian systems.
They found the hybrid skin-topological effect induced by gain and loss in two-dimensional systems. This kind of skin effect is selective, i.e., the bulk states and the edge states have different behavior. The bulk states are not affected by the skin effect and remain extended, while the edge states exhibit skin effect and are further localized to corners. This hybrid phenomenon of skin effect and topological effect shows the unique properties of non-Hermitian topological systems, which do not have Hermitian or nontopological analogs. As a specific example, they considered the non-Hermitian Haldane model with gain and loss [Fig. 1 (a)]. In the Haldane model, the topological edge states are obtained by introducing on-site energy and local magnetic flux. It is one of the two important models to realize the quantum anomalous Hall effect in condensed matter physics. They found that if staggered gain and loss are introduced into the nearest-neighbor sites in the Haldane model, the topological edge modes of the system will exhibit the skin effect and are localized to the corners, while the bulk modes are not affected. So, it reveals a hybrid skin-topological effect. By analyzing the lattice sites at the edges alone, this second-order skin-topological effect can be simplified to the first-order skin effect at the edges. In the simplified one-dimensional model, there are chiral edge currents due to the nonlocal magnetic flux introduced by the complex next-nearest-neighbor couplings. They are equivalent to non-reciprocal couplings, so the system exhibits the first-order skin effect [Fig. 1 (b) - (c)]. On the contrary, there is only local flux, and the non-reciprocity cancels out in the bulk of the system. So, the bulk modes are not affected by the skin effect. By adjusting the gain and loss of the system, the direction of edge currents can be changed, to control the direction of the skin-topological effect [Fig. 1 (d) - (f)].
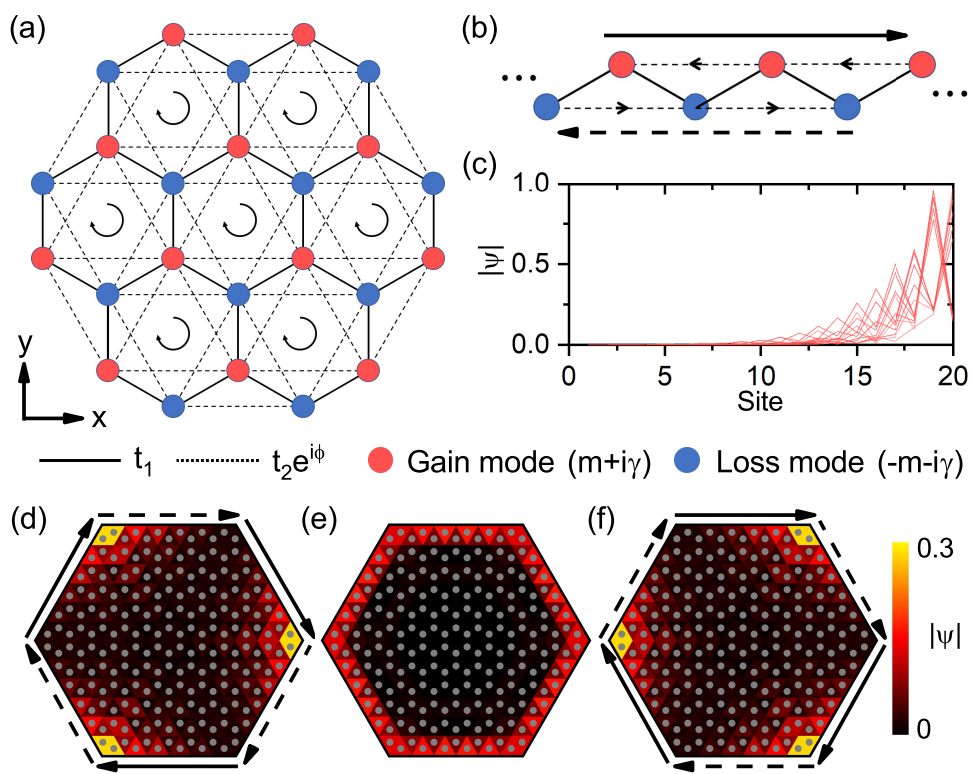
Fig. 1 Hybrid skin-topological modes in non-Hermitian Haldane model. (a) Schematic of the non-Hermitian lattice. The red (blue) circles denote sites with opposite on-site mass terms +(m+iγ). (b) Zigzag edge of the honeycomb lattice as a 1D chain, which has non-Hermitian skin effect with on-site gain and loss. The long solid (dashed) arrow indicates the chiral edge current along (opposite to) the localized direction [similar in (d) and (f)]. The black arrows in (a) and middle-line arrows in (b) indicate the directions of the next-nearest-neighbor couplings t2eiφ. (c) Profile of all eigenmodes for the 1D chain in (b) with 20 sites. The on-site gain and loss are γ=3. (d)-(f) The chiral edge mode for γ=0 (e) becomes skin-topological modes for γ=-0.6 (d) and γ=0.6 (f) with different localized directions. Every triangle with a grey circle denotes a site. Here the chiral edge mode propagates clockwise.
They further obtained the relationship between the parity-time (PT) symmetries of the system and the hybrid skin-topological effect. When choosing the open boundary condition and the periodic boundary condition in different directions, the system exhibits different kinds of PT symmetries for different kinds of edges. The global PT symmetry which maps any mode localized in one boundary into the other boundary precludes the emergence of the hybrid skin-topological effect, while the local PT symmetry with mapping inside each sub-cell allows the existence of the hybrid skin-topological effect. Therefore, the analysis of PT symmetries of the system provides a simple and effective means to judge whether there is the hybrid skin-topological effect. In particular, they found that when the gain and loss in the system increase, the PT phase transition will occur between the skin-topological modes, accompanied by the emergence of exceptional points (EPs). When PT symmetry is broken, the eigen energies of the skin-topological modes are no longer real and the distributions of the corresponding eigen modes become PT-asymmetric.
In addition, they studied the Chern numbers in the non-Hermitian system and obtained the phase diagram. They provided intuitionistic geometric meanings of the Chern numbers as topological invariants. As shown in Fig. 2(a), the two-dimensional Brillouin zone of the system can be mapped to a closed spherical surface S in the three-dimensional space, and the gap-closing points of the system form a circle L in the three-dimensional space. When the surface S encloses the circle L, the system is at the non-Hermitian Chern insulator phase, and the Chern number is 1, corresponding to the red region in Fig. 2(b). When the circle L is outside the surface S, the system is at the non-Hermitian conventional insulator phase, and the Chen number is 0, corresponding to the blue area in Fig. 2 (b). In the gray area in Fig. 2 (b), the system band gap is closed at six EPs.
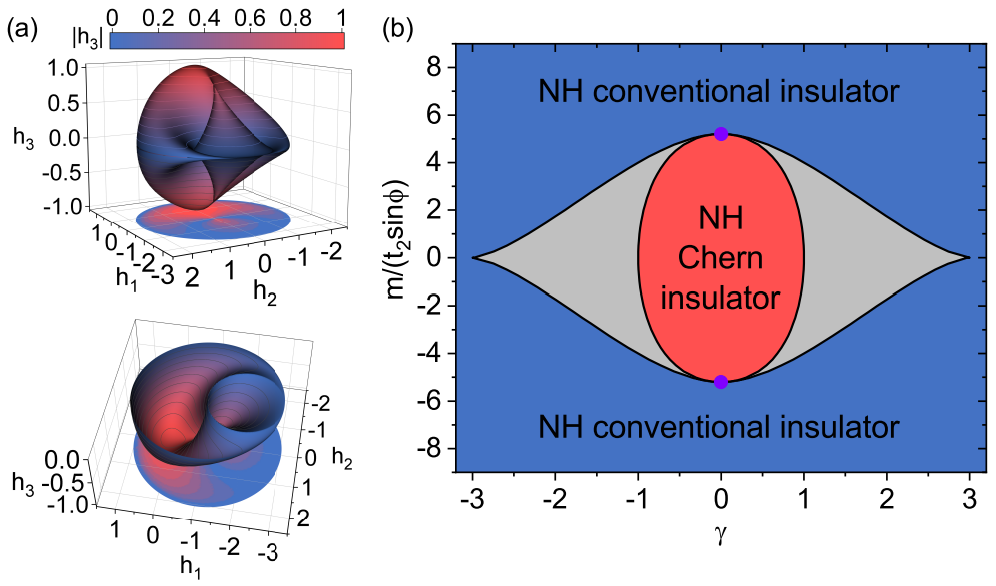
Fig. 2 The topology and phase diagram of the non-Hermitian Haldane model. (a) The surface S mapped from the first Brillouin zone, i.e., mapping from (kx, ky) to (h1, h2, h3). The color map represents the magnitude of h3. The density map below is the projection of the surface. The bottom figure is half of the top figure for h3<0. (b) The phase diagram. The red area is the non-Hermitian Chern insulator phase where C=1. The blue area is the non-Hermitian conventional insulator phase where C=0. The gray area is a gapless phase with EPs between two bulk bands. The black curves are phase boundaries. The purple points indicate the Hermitian phase boundary with the emergence of Dirac points.
The conclusion of this work is also applicable to the system with no gain and only pure dissipation. Dissipation is common in many physical systems, such as optical systems, atomic systems, and optomechanical systems. This work paves the way to realize non-Hermitian topological effect by gain and loss and study PT phase transition in higher-dimensional systems. It also provides attractive insights for potential applications in topological optics.
The first author of the paper is graduate student Yaohua Li, and the corresponding author is Associate Prof. Yong-Chun Liu, both from the Department of Physics, Tsinghua University. This work is supported by the Key-Area Research and Development Program of Guangdong Province, the National Natural Science Foundation of China (NSFC), and the National Key R&D Program of China.
Research link: https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.128.223903
Yaohua Li, Chao Liang, Chenyang Wang, Cuicui Lu, and Yong-Chun Liu*, Gain-loss-induced hybrid skin-topological effect, Phys. Rev. Lett. 128, 223903 – Published 1 June 2022
Editors: John Olbrich, Li Han

